Дерево
Дерево – это связный ациклический граф, содержащий \(n\) вершин и \(n-1\) рёбер. Удаление любого ребра разбивает дерево на две компоненты связности, а добавление любого ребра создает цикл. Между любыми двумя вершинами дерева существует единственный путь.
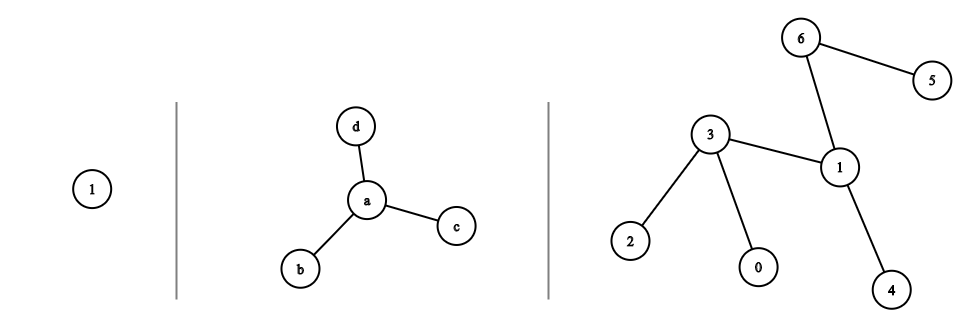
На рисунке выше изображены три дерева. У левого дерева \(1\) вершина, у среднего – \(4\) вершины, у правого – \(7\) вершин.
Теорема. Пусть \(G\) – неориентированный граф, тогда из любой пары трёх утверждений следует третье (и истинность любой пары фактов — критерий того, что \(G\)является деревом):
● \(n=m+1\) (\(n\) – количество вершин, \(m\) – количество рёбер);
● \(G\) – связный граф;
● \(G\) – ациклический (не содержит простых циклов).
Таким образом, если необходимо проверить заданный граф на то, является ли он деревом, то вы сами можете выбрать любые два требования из трёх для проверки. Обычно проще всего проверить первые два требования.
Листьями дерева называются вершины, имеющие только одного соседа. В каждом дереве найдется не менее одного листа (а, если в дереве \(n>1\), то не и менее двух листьев).
В корневом дереве одна из вершин считается корнем дерева, а все остальные располагаются под ней. Вершины, расположенные непосредственно под некоторой вершиной, называются ее дочерними вершинами, а вершина, расположенная непосредственно над некоторой вершиной, – её родителем. У каждой вершины, кроме корня, имеется ровно один родитель. У корня родителя нет. Корневое дерево имеет рекурсивную структуру: каждая вершина играет роль корня поддерева, содержащего эту вершину и все вершины, принадлежащие поддеревьям ее дочерних вершин.
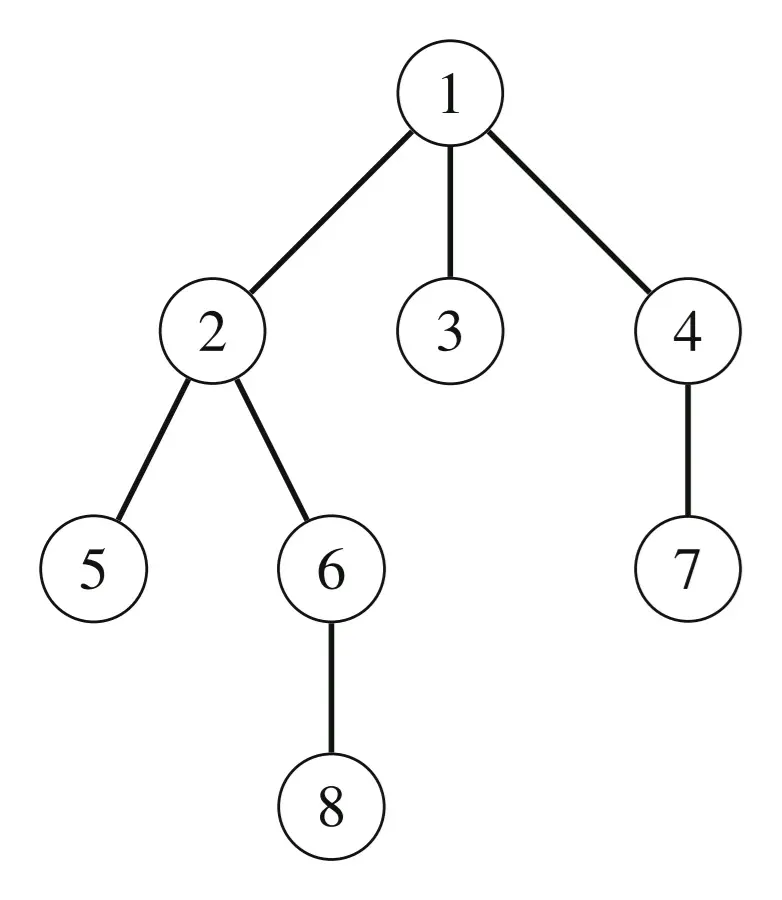
На рисунке выше показано корневое дерево с корнем в вершине \(1\). Дочерними для вершины \(2\) являются вершины \(5\) и \(6\), а родителем вершины \(2\) – вершина \(1\). Поддерево вершины \(2\) состоит из вершин \(2,5,6\) и \(8.\)
Сумма степеней всех вершин дерева равна удвоенному числу рёбер:
\(\displaystyle\sum_{v\in V}deg(v)=2\cdot (n-1)\)
Лес — это такой граф, каждая компонента связности которого является деревом. Количество компонент связности леса равно \(n-m.\)
