Жадные алгоритмы

Жадный алгоритм — алгоритм, заключающийся в принятии локально оптимальных решений на каждом этапе, допуская, что конечное решение также окажется оптимальным.

Задача "Размен монет"

Монетная система некоторого государства состоит из монет достоинством $a_1 = 1 < a_2 < \ldots < a_n$. Требуется выдать сумму $S$ наименьшим возможным количеством монет.

Жадный алгоритм решения этой задачи таков. Берётся наибольшее возможное количество монет достоинства $a_n : x_n = \lfloor \frac{S}{a_n} \rfloor$. Таким же образом получаем, сколько нужно монет меньшего номинала, и т. д.

Для данной задачи жадный алгоритм не всегда даёт оптимальное решение, а только для некоторых, называемых каноническими, монетных систем, вроде используемых в США ($1$, $5$, $10$, $25$ центов). Неканонические системы таким свойством не обладают. Так, например, сумму в $24$ копейки монетами в $1$, $5$ и $7$ коп. жадный алгоритм разменивает так: $7$ коп. — $3$ шт., $1$ коп. — $3$ шт., в то время как правильное решение — $7$ коп. — $2$ шт., $5$ коп. — $2$ шт.

Пример

У кассира есть бесконечное количество монет номиналами $1$, $5$, $10$. Выведите минимальное количество монет, чтобы выдать сдачу $money$.

Решение:

Рассмотрим основную идею решения. Пока сдача положительна $money > 0$, мы выбираем монету с самым большим номиналом, не превышающем $money$, отнимаем значение номинала выбранной монеты от $money$ и увеличиваем количество монет:

money = int(input())

cnt = 0
while money > 0:
  if money >= 10:
    money -= 10
  elif money >= 5:
    money -= 5
  else:
    money -= 1
  cnt += 1

print(f"{cnt}")

26
4

Также эту задачу можно решить в одну строку:

cnt = money // 10 + money % 10 // 5 + money % 5

Проектировать жадные алгоритмы просто, но вот доказывать их правильность — нередко сложная задача.

Задача "Специи"

Вор пробрался в лавку специй и нашёл там четыре фунта шафрана, три фунта ванили и пять фунтов корицы. В его рюкзак можно сложить до девяти фунтов, поэтому забрать всё он не сможет. Предположим, что цены на шафран, ваниль и корицу $$5000$, $$200$ и $$10$ соответственно. Как унести максимально дорогую добычу? Если вор заберёт $u_1$ фунтов шафрана, $u_2$фунтов ванили и $u_3$ фунтов корицы, общая ценность украденного составит $5000 \cdot \frac{u_1}{4} + 200 \cdot \frac{u_2}{3} + 10 \cdot \frac{u_3}{5}.$ Вор хотел бы найти максимальное значение этого выражения при следующих ограничениях: $u_1 \leq 4, u_2 \leq 3, u_3 \leq 5, u_1 + u_2 + u_3 \leq 9.$

Решение:

Определим цену специи $i$ как $\frac{c_i}{w_i}$. Естественной стратегией для вора было бы брать как можно больше самой дорогой специи.

Чтобы доказать, что эта стратегия приводит к оптимальному решению, рассмотрим самую дорогую специю $m$. Каков максимальный объём $a$ $m$-й специи, который вор может положить в рюкзак?

Во-первых, она должна уместиться в рюкзак: $a \leq W.$

Во-вторых, она не должна превышать доступный объём $m$-й специи: $a \leq w_m.$

Следовательно, $a = min(w_m, W)$ Мы утверждаем, что существует оптимальное решение, включающее в себя $a$ фунтов $m$-й специи.

Доказав, что мы можем взять самой дорогой специи столько, сколько получится, мы можем спроектировать жадный алгоритм: взять как можно больше самой дорогой специи и повторить. Мы прекратим, когда больше не останется специй или когда рюкзак будет заполнен до конца.

Задача "Рекламная кампания"

Представим, что вы владелец популярной страницы в интернете, на которой есть $n = 3$ рекламных мест. Вы хотите продать их рекламодателям, которые рассчитывают на $clikcs_1 = 10, clikcs_2 = 20, clikcs_3 = 30$ кликов в день и при этом готовы платить $price_1 = 2, price_2 = 3, price_3 = 5$ за клик. Как подобрать пары рекламных мест и рекламодателей так, чтобы получить максимальную прибыль?

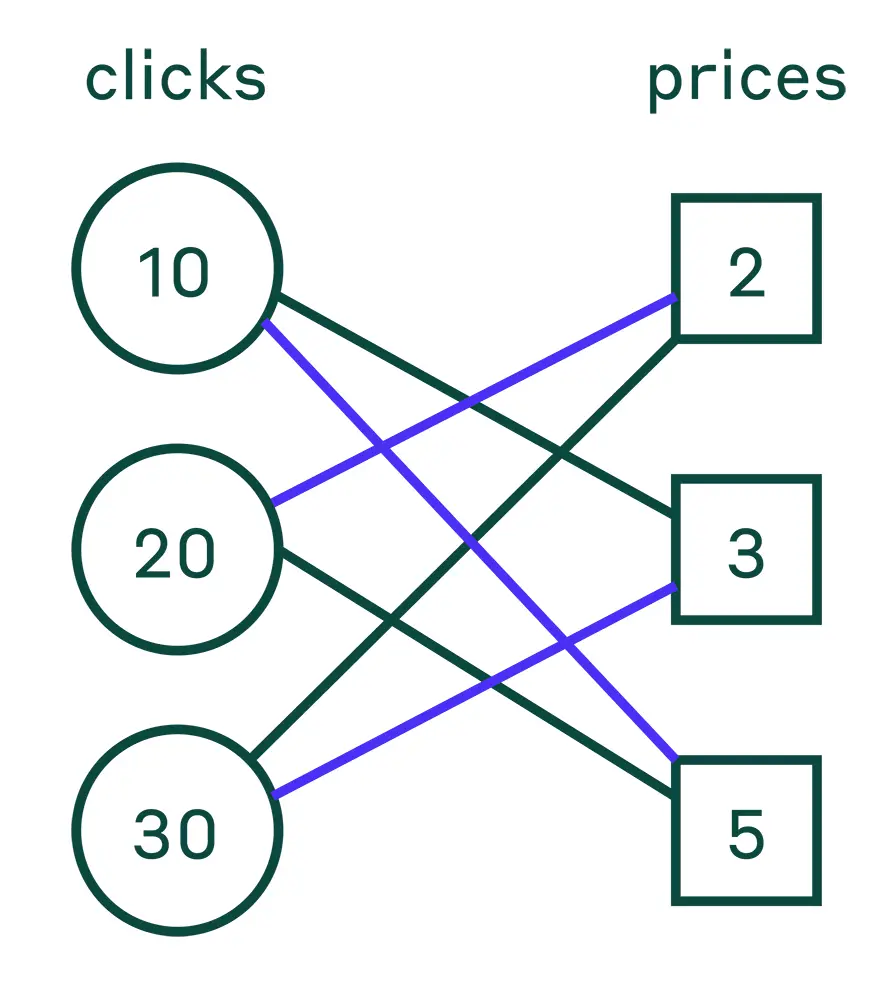
Например, доход от отмеченных голубым цветом пар, приведённых выше, составит $10 \cdot 5 + 20\cdot 2 + 30\cdot 3 = 180$ долларов; от отмеченных чёрным — $10 \cdot 3 + 20\cdot 5 + 30\cdot 2 = 190.$

Решение:

Суть решения заключается в том, чтобы отдать самое популярное рекламное место самому дорогому объявлению. Вас вряд ли удивит, что жадный подход даст максимальную прибыль.

Это приводит нас к алгоритму, который объединяет рекламное объявление с максимальным количеством кликов за максимальную цену, исключает их из вариантов на рассмотрение и повторяет то же самое.

Практические задания

Авторизация