Метрики
Метрика определяет расстояние между двумя точками. Обычное евклидово расстояние между точками \((x_1, y_1)\) и \((x_2, y_2)\) равно
\(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.\)
Манхэттенское расстояние между точками \((x_1, y_1)\) и \((x_2, y_2)\) вычисляется по формуле
\(|x_1 - x_2| + |y_1 - y_2|\)
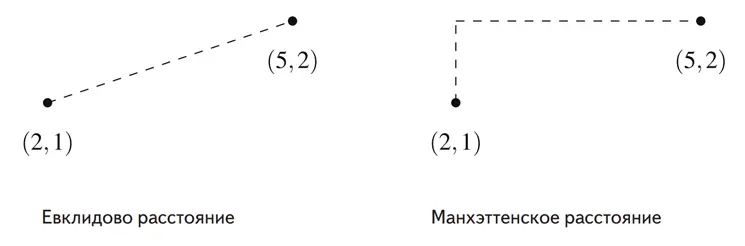
На рисунке ниже евклидово расстояние между точками равно
\(\sqrt{(5 - 2)^2 + (2 - 1)^2} = \sqrt{10},\)
а манхэттенское расстояние между ними же равно
\(|5 - 2| + |2 - 1| = 4.\)
На рисунке ниже показано, как выглядят единичные круги – множества точек, удаленных от центра на расстояние, не большее \(1\), – при использовании евклидовой и манхэттенской метрик.

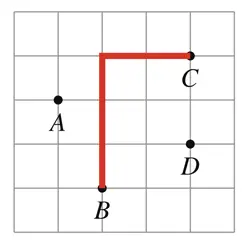
Некоторые задачи проще решить, если использовать манхэттенское, а не евклидово расстояние. Например, пусть дано множество точек на плоскости и требуется найти пару точек, для которых манхэттенское расстояние максимально. Так, на рисунке ниже манхэттенское расстояние между точками \(B\) и \(C\) максимально и равно \(5\).
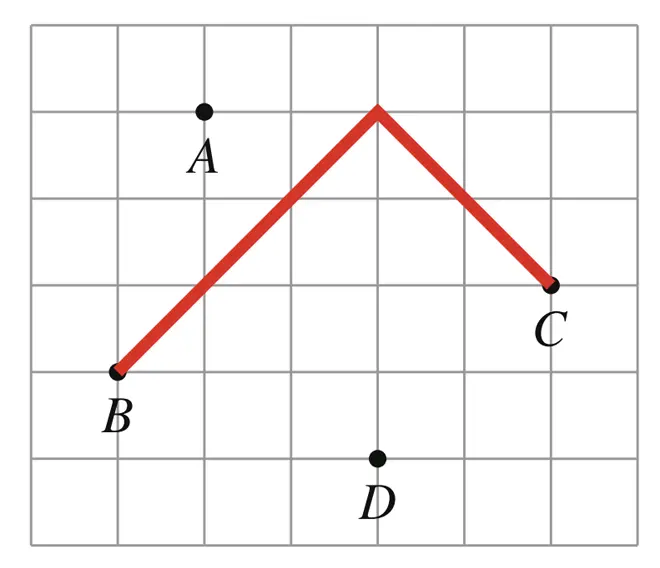
При работе с манхэттенским расстоянием бывает полезно применить преобразование координат \((x, y) \to (x + y, y − x)\). При этом происходят поворот на \(45^{\circ}\) и масштабирование. На рисунке ниже показан результат этого преобразования в нашем примере.
Рассмотрим теперь две точки \(p_1 = (x_1, y_1) \) и \(p_2= (x_2, y_2) \), которые после преобразования перешли в \(p'_1 = (x'_1, y'_1)\) и \(p'_2 = (x'_2, y'_2)\). Манхэттенское расстояние между \(p_1\) и \(p_2\) можно выразить двумя способами:
\(|x_1 - x_2| + |y_1 - y_2| = max(|x'_1 - x'_2|, |y'_1 - y'_2|)\)
Например, если \(p_1 = (1, 0)\) и \(p_2 = (3, 3)\), то преобразованные координаты равны \(p'_1 = (1, -1)\) и \(p'_2 = (6, 0)\), а манхэттенское расстояние
\(|1 - 3| + |0 - 3| = max(|1 - 6|, |-1 - 0|) = 5.\)
Преобразование координат дает простой способ работать с манхэттенскими расстояниями, потому что координаты x и y можно рассматривать порознь. В частности, чтобы максимизировать манхэттенское расстояние, необходимо найти такие две точки, что их преобразованные координаты доставляют максимум величине
\(max(|x'_1 - x'_2|, |y'_1 - y'_2|).\)
Это легко, потому что должна быть максимальна разность горизонтальных или вертикальных координат после преобразования.
Пример 1
Найдите евклидово расстояние между точками \(p_1\) и \(p_2\).
from math import dist
p1 = list(map(int, input().split()))
p2 = list(map(int, input().split()))
d1 = dist(p1, p2) # с использованием функции dist
d2 = ((p1[0] - p2[0]) ** 2 + (p1[1] - p2[1]) ** 2) ** 0.5 # по формуле
print(f"{d1:.2f}\n{d2:.2f}")
2 1
5 2
3.16
3.16
Пример 2
Найдите манхэттенское расстояние между точками \(p_1\) и \(p_2\).
p1 = list(map(int, input().split()))
p2 = list(map(int, input().split()))
d = abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])
print(f"{d}")
2 1
5 2
4
