Компьютерный центр г. Светлогорска

При решении многих практических задач приходится выполнять деление различных предметов на равные части:

Возникает вопрос: как обозначить, на сколько равных частей разделили предмет и сколько частей взяли? Для обозначения равных частей целого используют дробные числа, или дроби.

Разделим круг на \(6\) равных частей и из них возьмём две части:

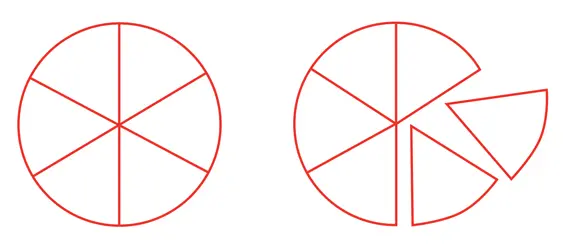
Для обозначения двух равных частей из шести потребуются два натуральных числа:

1. Первое число показывает, на сколько равных частей разделили предмет.
2. Второе число показывает, сколько таких частей взяли.

Для записи нового числа используется дробная черта: над чертой записывают число \(2\), а под чертой — число \(6\). Получаем запись дроби \(\frac26\). Читается: «две шестых».

Число, записанное под чертой дроби, показывает, на сколько равных частей разделили предмет. Оно называется знаменателем дроби.

Число, записанное над чертой дроби, показывает, сколько таких частей взяли. Оно называется числителем дроби.

Чтобы найти значение дроби, необходимо числитель разделить на знаменатель. Например, значением дроби \(\frac12\) является число \(0.5\).

В парке \(n\) кустов роз. Из них \(\frac23\) подготовили к зимнему периоду. Сколько кустов роз подготовили к зимнему периоду?

Решение:

Дробь \(\frac23\) указывает на то, что всё количество кустов роз разделено на три равные части и взяты \(2\) такие части.

n = int(input())
k = n // 3 * 2
print(f"{k}")

120
80

В соревнованиях по армрестлингу в лагере отдыха приняли участие \(n\) ребят из первого отряда, что составляет \(\frac25\) всех участников. Сколько участников соревновалось?

Решение:

Дробь \(\frac25\) показывает, что число всех участников соревнования разделили на \(5\) равных частей и взяли \(2\) части. Эти две части составляют \(n\) человек. Для того чтобы найти количество всех участников, нужно узнать, сколько человек приходится на \(5\) частей.

n = int(input())
k = n // 2 * 5
print(f"{k}")

12
30

a = int(input())
b = int(input())
c = int(input())
d = b + c
e = a / d
print(f"{e:.1f}")

1
2
3
0.2

Чтобы узнать, во сколько раз одно число больше другого, выполняют деление большего числа на меньшее.

Например: в шестых классах гимназии учатся \(120\) человек, а в десятых —  \(40\). Во сколько раз шестиклассников больше?

Полученное при решении задачи частное \(120 : 40\) можно записать в виде дроби \(\frac{120}{40}\). Дробь получается и при вычислении дробного отношения двух чисел. Таким образом, результат деления двух чисел \(a\) и \(b\) можно прочитать как отношение чисел \(a\) и \(b\) или отношение \(a\) к \(b\).

Верное равенство двух отношений называется пропорцией:

Она может быть прочитана так: отношение \(a\) к \(b\) равно отношению \(c\) к \(d\) или так: \(a\) относится к \(b\) так же, как \(c\) относится к \(b\).

Пропорция может быть записана в виде:

Числа \(a, b, c, d\) называются членами пропорции: \(a\) и \(d\) — крайние члены пропорции, \(b\) и \(c\) — средние члены пропорции.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению средних членов пропорции. Можно использовать такую запись:

Для холодной засолки \(12\) кг грибов берут \(600\) г соли. Сколько грамм соли понадобится, чтобы засолить \(n\) кг грибов?

Решение:

Если масса грибов увеличивается в некоторое число раз, то и количество соли для засолки грибов этой массы грибов увеличивается в такое же число раз. Так как отношение массы грибов равно отношению массы соли, то можно составить пропорцию: \(\frac{12}n = \frac{600}x\)

n = int(input())
x = n * 600 // 12
print(f"{x}")

40
2000

Четверо рабочих могут выполнить работу за \(n\) дней. За сколько дней смогут сделать эту же работу \(6\) рабочих?

Решение:

Если количество рабочих увеличивается в некоторое число раз, то количество дней, необходимых им для выполнения работы, уменьшается в такое же число раз. Составим пропорцию: \(\frac46 = \frac{x}n\)

n = int(input())
x = 4 * n // 6
print(f"{x}")

12
8

На сколько процентов понизились цены на товары и услуги? Каков процент по кредиту, предоставляемого в банке? Сколько процентов посевных полей использовано для выращивания пшеницы? Эти и многие другие вопросы из повседневной жизни связаны с понятием процента. Выясним, что называется процентом и как используется это понятие для решения практических задач.

Дробь \(\frac1{100}\) называется один процент. Обозначается: \(\frac1{100}=1\%\).

Число процентов можно записать в виде дроби: \(43\% = \frac{43}{100}; 6\% = \frac{6}{100}\).

Обратно, всякую дробь можно записать в виде числа процентов. Для этого нужно дробь умножить на \(100\%\): \(0.04 \cdot 100\% = 4\%; \; \frac45 \cdot 100\% = 80\%\)

1. Нахождение процента m от числа a:

    

   \(b = \frac{a}{100} \cdot m\%\)

    

2. Нахождение числа a по его проценту m:

    

   \(a = \frac{b}{m\%} \cdot 100\%\)

    

3. Нахождение процентного отношения чисел (какой процент одно число b составляет от другого a:

    

   \(m\% = \frac{b}{a} \cdot 100\%\)

    

В школьном саду \(n\) деревьев. Яблони составляют \(50\%\) всех деревьев. Сколько яблонь в школьном саду?

n = int(input())
k = n * 50 // 100
print(f"{k}")

400
200

x = 0.3 * 3 + 0.1
print(f"{x:.20f}")  # 0.99999999999999988898

Даны \(3\) целых положительных числа \(a,b,c.\) Сравните дроби \(\frac{a}{b}\) и \(\frac{a+c}{b+c}\) и выведите результат сравнения.

Решение:

Можно сначала подумать: «сравним значения дробей напрямую, вычислив \(\frac{a}{b}\) и \(\frac{a+c}{b+c}\) в вещественном виде». Но при работе с плавающей точкой появляются ошибки округления — поэтому давайте попробуем решить без применения вещественных чисел. Сравним аккуратно дроби: \(\frac{a}{b} < \frac{a+c}{b+c} \Leftrightarrow a\cdot(b+c)<b\cdot(a+c).\) Раскроем скобки: \(ab+ac<ab+bc \Leftrightarrow ac<bc.\) Так как \(c >0\) по условию, то из \(ac<bc\) следует \(a<b.\) Таким образом:

● если \(a<b,\) то \(\frac{a}{b} < \frac{a+c}{b+c};\)

● если \(a>b,\) то \(\frac{a}{b} > \frac{a+c}{b+c};\)

● если \(a=b,\) то \(\frac{a}{b} = \frac{a+c}{b+c}.\)

То есть вся задача сводится к простому сравнению целых \(a\) и \(b\) — никаких делений и никаких ошибок с вещественными числами.

a, b, c = map(int, input().split())

if a > b:
    print(f">")
elif a < b:
    print(f"<")
else:
    print(f"=")

1 2 3
<

Маша наблюдает из дома за грозой. Она увидела молнию, а через \(t\)  секунд услышала гром от молнии. Она знает, что в той стороне, где была молния, есть одинокое дерево, и боится, не попала ли молния в это дерево. Расстояние от Машиного дома до дерева равно \(r\)  метров, скорость звука равна \(v\)  метров в секунду, скорость света считаем бесконечной. Определите, могла ли молния попасть в дерево. Выведите YES, если молния могла попасть в дерево, и NO в противном случае.

Решение:

Расстояние от дома Маши до молнии равно \(v \cdot t.\) Осталось проверить, равно ли это \(r.\) Можно было бы написать if v * t == r, но, поскольку все числа вещественные, так просто не заработает — из-за погрешностей результат умножения может оказаться не равен \(r\), даже если на самом деле он должен быть равен. Поэтому надо проверять, что \(v \cdot t\) примерно равно \(r\), т.е. что разница abs(r - v * t) не слишком велика. Выберем какое-нибудь eps и будем сравнивать с ним. Итоговый код:

t, v, r = map(float, input().split())

eps = 1e-6
if abs(r - v * t) < eps:
    print("YES")
else:
    print("NO")
    
# С помощью функции isclose

from math import isclose

t, v, r = map(float, input().split())

if isclose(r, v * t):
    print(f"YES")
else:
    print(f"NO")

2.5 300.0 750.0
YES

Практические задания