Компьютерный центр г. Светлогорска

Двумерный список — это одномерный список, элементами которого являются одномерные списки. Другими словами, это набор однотипных данных, имеющий общее имя, доступ к элементам которого осуществляется по двум индексам. Наглядно двумерный список удобно представлять в виде таблицы, в которой n строк и m столбцов, а под ячейкой таблицы, стоящей в i-й строке и j-м столбце понимают некоторый элемент списка a[i][j].

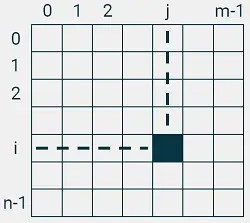
Действительно, если разобраться с тем, что такое a[i] при фиксированном значении i, то увидим, что это одномерный список, состоящий из \(m\) элементов, к которым можно обращаться по индексу:

a[i][0], a[i][1], …, a[i][m-1]

Схематически это вся i-я строка таблицы. Аналогично, если мы рассмотрим одномерный список строк, то сможем заметить, что это так же двумерный список, где каждый отдельный элемент — это символ, а a[i] —  это одномерный список, представляющий отдельную строку исходного одномерного списка строк.

По-другому двумерный список также называют матрицей, а в том случае, когда n=m (число строк равно числу столбцов) матрицу называют квадратной. В матрицах можно хранить любые табличные данные. Матрицы часто используют для решения олимпиадных и математических задач.

Для ввода матрицы размера n×m можно использовать следующие конструкции:

a = [list(map(int, input().split())) for i in range(n)]  # ввод матрицы целых чисел
a = [list(map(float, input().split())) for i in range(n)]  # ввод матрицы вещественных чисел
a = [input().split() for i in range(n)]  # ввод матрицы слов
a = [input() for i in range(n)]  # ввод матрицы букв

Для вывода элементов матрицы можно использовать цикл for с применением распаковки списка:

numbers = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
for row in numbers:
    print(*row)

или использовать двойной цикл:

numbers = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

#  По индексам
for i in range(3):
    for j in range(3):
        print(f"{a[i][j]}", end=" ")
    print()

#  По элементам
for row in numbers:
    for col in row:
        print(f"{col}", end=" ")
    print()

1 2 3
4 5 6
7 8 9

Самые распространенные и простые способы обхода элементов матрицы: по строкам и столбцам.

Обход по строкам сверху вниз:

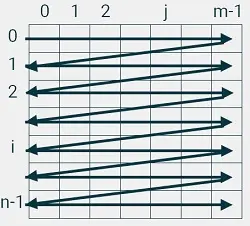
a = [[1, 2, 3], [4, 5, 6]]
for i in range(2):
    for j in range(3):
        print(f"{a[i][j]}", end=" ")

1 2 3 4 5 6 

Обход по столбцам слева направо:

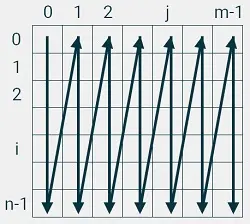
a = [[1, 2, 3], [4, 5, 6]]
for j in range(3):
    for i in range(2):
        print(f"{a[i][j]}", end=" ")

1 4 2 5 3 6 

Дана матрица a размера n×m. Поверните её против часовой стрелки на \(90\) градусов.

n, m = map(int, input().split())
a = [list(map(int, input().split())) for _ in range(n)]

print(f"{m} {n}")
for j in range(m - 1, -1, -1):
    for i in range(n):
        print(f"{a[i][j]}", end=' ')
    print()

3 4
1 2 3 4
5 6 7 8
9 10 11 12

4 3
4 8 12 
3 7 11 
2 6 10
1 5 9

Дана квадратная матрица a размера n×n. Найдите сумму её однозначных чисел.

n = int(input())
a = [list(map(int, input().split())) for _ in range(n)]

s = 0
for ai in a:
    for aij in ai:
        if -9 <= aij <= 9:
            s += aij
print(f"{s}")

3
5 0 12
0 -10 -5
1 9 -100

10

Дана матрица латинских строчных букв a размера n×m. Найдите количество гласных букв в её подматрице, где (r1,c1) – левый верхний элемент и (r2,c2) – правый нижний элемент. Нумерация индексов начинается с \(1.\)

n, m = map(int, input().split())
a = [input() for _ in range(n)]
r1, c1, r2, c2 = map(int, input().split())

k = 0
for i in range(r1 - 1, r2):
    for j in range(c1 - 1, c2):
        if a[i][j] in 'aeiouy':
            k += 1
print(f"{k}")

4 5
kcdim
print
mouse
input
2 2 3 4

3

Дана квадратная матрица слов a размера n×n. Выведите YES, если все слова в матрице состоят из чётного количества букв, иначе выведите NO.

n = int(input())
a = [input().split() for _ in range(n)]

ans = "YES"
for ai in a:
    for aij in ai:
        if len(aij) % 2 == 1:
            ans = "NO"
print(f"{ans}")

2
code byte
test java

YES

2
data error
flag loop

NO

Практические задания

Дана квадратная матрица a размера n×n. Обменяйте строки k1 и k2.

n = int(input())
a = [list(input().split()) for i in range(n)]
k1, k2 = map(int, input().split())

k1 -= 1
k2 -= 1
for i in range(n):
    for j in range(n):
        if i == k1:
            print(f"{a[k2][j]}", end=' ')
        elif i == k2:
            print(f"{a[k1][j]}", end=' ')
        else:
            print(f"{a[i][j]}", end=' ')
    print()

3
1 2 3
4 5 6
7 8 9
1 2

4 5 6 
1 2 3 
7 8 9 

Дана матрица a размера n×m. Выведите количество однозначных чисел в каждом столбце.

n, m = map(int, input().split())
a = [list(map(int, input().split())) for i in range(n)]
for j in range(m):
    k = 0
    for i in range(n):
        if -9 <= a[i][j] <= 9:
            k += 1
    print(f"{k}", end=' ')

4 3
1 2 3
-9 15 10
-10 0 -13
6 123 -100

3 2 1 

Дана матрица a размера n×m. Выведите сумму нечётных чисел в строке k.

n, m = map(int, input().split())
k = int(input())
a = [list(map(int, input().split())) for i in range(n)]
k -= 1
s = 0
for j in range(m):
    if a[k][j] % 2 == 1:
        s += a[k][j]
print(f"{s}")

3 3
3
1 2 3
4 5 6
7 8 9

16

Дана квадратная матрица a размера n×n. В каждой строке найдите наименьший элемент.

n = int(input())
a = [list(map(int, input().split())) for i in range(n)]
for i in range(n):
    mi = a[i][0]
    for j in range(n):
        if a[i][j] < mi:
            mi = a[i][j]
    print(f"{mi}")

3
1 3 2
6 5 4
9 7 8

1
4
7

Дана квадратная матрица символов a размера n×n. Выведите YES, если в столбце k есть заглавная латинская буква, иначе выведите NO.

n = int(input())
a = [input() for i in range(n)]
k = int(input())
k -= 1
ans = "NO"
for i in range(n):
    if 'A' <= a[i][k] <= 'Z':
        ans = "YES"
        break
print(f"{ans}")

3
Abc
deF
ghi
2

NO

3
Abc
deF
gHi
2

YES

Практические задания

У квадратной матрицы есть две диагонали:

1. главная: проходит из верхнего левого в правый нижний угол матрицы;
2. побочная: проходит из нижнего левого в правый верхний угол матрицы.

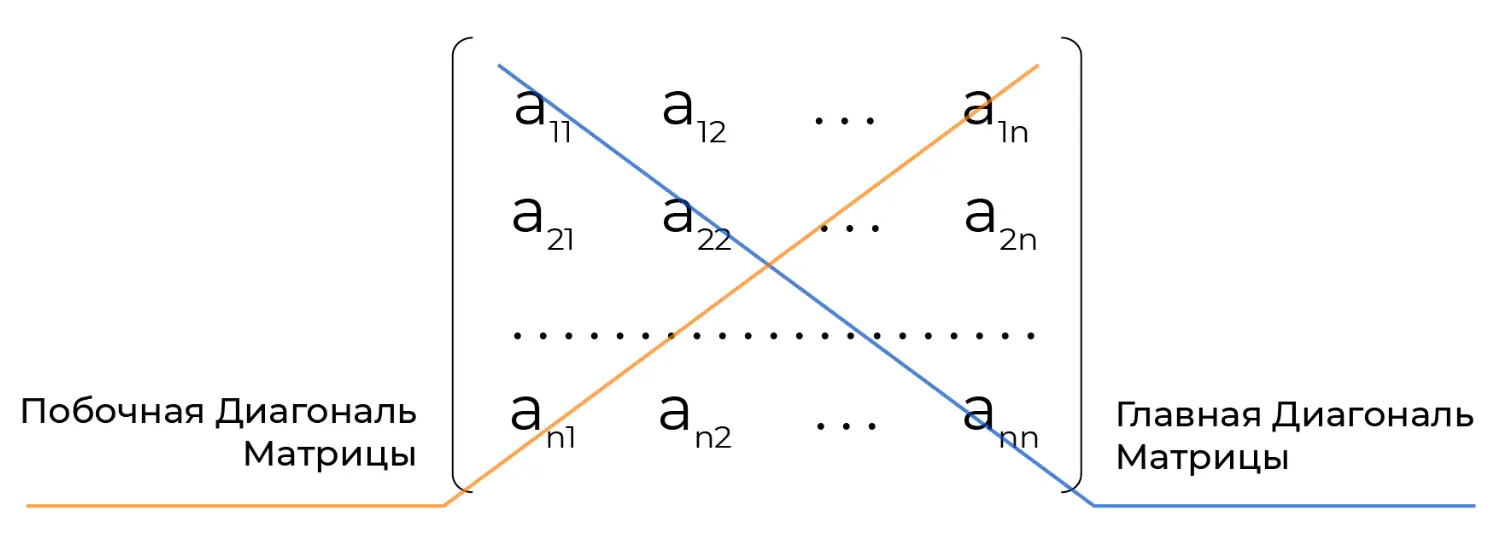
Элементы с равными индексами i=j находятся на главной диагонали. Такие элементы обозначаются a[i][i].

Элементы с индексами i и j, связанными соотношением i+j=n-1 (или j=n-i-1), где n — размерность матрицы, находятся на побочной диагонали.

Заметим также, что:

● если элемент находится выше главной диагонали, то i<j; если ниже, то i>j.

● если элемент находится выше побочной диагонали, то i+j<n-1; если ниже, то i+j>n-1.

Таким образом, чтобы обойти элементы главной или побочной диагонали, достаточно одного цикла.

Дана квадратная матрица a размера n×n. Выведите в одну строку элементы главной диагонали.

n = int(input())
a = [list(map(int, input().split())) for i in range(n)]

for i in range(n):
    print(f"{a[i][i]}", end=' ')

3
1 2 3
4 5 6
7 8 9

1 5 9

Дана квадратная матрица строчных латинских букв a размера n×n. Найдите количество гласных букв побочной диагонали матрицы.

n = int(input())
a = [input() for i in range(n)]

k = 0
for i in range(n):
    if a[i][n-i-1] in 'aeiouy':
        k += 1
print(f"{k}")

5
hello
kcdim
mouse
input
dream

3

Практические задания